← CPL WASM に戻る | English | GitHub

CPL チュートリアル

CPL チュートリアル

はじめに

CPL (Categorical Programming Language) は、圏論の概念に基づいて設計されたプログラミング言語です。CPLでは、通常のプログラミング言語で「データ型」や「関数」と呼ばれるものが、圏論における「対象」と「射」として扱われます。

集合論 関数型プログラミング CPL
集合 データ型 対象
写像 関数 射

CPLの特徴

前提知識

このチュートリアルでは、以下の知識があると理解しやすいでしょう:

圏論の知識は必要ありません。このチュートリアルを通じて、CPLの使い方とともに圏論の基本的な概念を学ぶことができます。

このチュートリアルで学べること

目次

基本的なコマンド

CPLのREPL (Read-Eval-Print Loop) では、以下のコマンドを使用します。このセクションでは概要のみを説明し、詳細は実際の使用例の中で学んでいきます。

初期画面

起動すると以下のような画面になります。

Categorical Programming Language (Haskell version)
version 0.1.0

Type help for help

cpl>

終対象の定義

CPLには組み込みのデータ型がなく、全てのデータ型は明示的に定義する必要があります。

何をするにも、他の関数型言語におけるユニット型に相応する終対象 (terminal object) が必ず必要なため、まずはこれを定義します。

圏論において、終対象 1 とは「どの対象 X からも、ただ一つだけ射が存在する対象」のことです。これは「終点」のような役割を果たし、情報を持たない（あるいは唯一の値しか持たない）対象を表します。ただ一つだけ存在する射を ! と書きます。

図式で描くと以下のような状況です。

プログラミングとの対応:

それでは、CPLで終対象を定義します。 edit コマンドを用いて、複数行編集モードに入り、データ型の定義を入力し、セミコロン ; で複数行編集モードを終了します。

cpl> edit
| right object 1 with !
| end object;
right object 1 defined

right object 1 defined と出力され、終対象 1 が定義できました。

定義された対象の詳細な情報は show object を用いて表示することができます。

cpl> show object 1
right object 1
- natural transformations:
- factorizer:
    
    ----------
    !: *a -> 1
- equations:
    (RFEQ): 1=!
    (RCEQ): g=!
- unconditioned: yes
- productive: ()

対象 1 が定義されると同時に任意の対象から終対象への特別な射 ! も定義されています。

show コマンドを使うことでも、射の型(定義域と余域)を表示することができます。 ここで *a は対象を表す変数で、したがってこれは任意の対象から終対象 1 への射を表しています。

cpl> show !
!
    : *a -> 1

直積の定義

続いて、 直積 (product) を定義します。直積は、二つの対象を組み合わせて一つの対象を作る操作です。

圏論において、直積 A × B (CPLでは prod(a,b)) は「二つの対象 A と B の情報を両方とも保持する対象」として定義されます。これは以下の性質を持ちます:

図式として描くと以下のようになります：

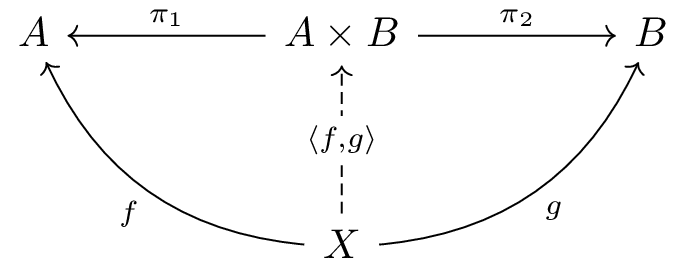
プログラミングとの対応:

それでは、CPLで直積を定義します：

cpl> edit
| right object prod(a,b) with pair is
|   pi1: prod -> a
|   pi2: prod -> b
| end object;
right object prod(+,+) defined

（ここで pi1, pi2 の定義域では、今定義しようとしている対象 prod については引数を省略して書くことになっていることに気をつけてください。これは「x -> a, x -> b を備えた x の中で最も普遍的なものを prod(a,b) と定義する」という意図ですが、x という名前を新たに導入することを避けて、prod という名前を再利用していると考えると良いでしょう）

終対象の場合と違って、直積は prod(a,b) はパラメータを取る対象になっており、定義結果では prod(+,+) と表示されます。 + は共変性を表し、 prod は2引数で、どちらの引数についても共変であることが分かります。 show object を用いて詳細を表示します。

cpl> show object prod
right object prod(+,+)
- natural transformations:
    pi1: prod(*a,*b) -> *a
    pi2: prod(*a,*b) -> *b
- factorizer:
    f0: *a -> *b  f1: *a -> *c
    ------------------------------
    pair(f0,f1): *a -> prod(*b,*c)
- equations:
    (REQ1): pi1.pair(f0,f1)=f0
    (REQ2): pi2.pair(f0,f1)=f1
    (RFEQ): prod(f0,f1)=pair(f0.pi1,f1.pi2)
    (RCEQ): pi1.g=f0 & pi2.g=f1 => g=pair(f0,f1)
- unconditioned: yes
- productive: (yes,yes)

終対象の場合と異なり、直積の場合には射影を表す二つの射 pi1, pi2 が同時に定義されています（show コマンドでも型を確認してみましょう）。

また、 f: a -> b と g: a -> c から pair(f,g): a -> prod(b,c) を作る関数 (ファクトライザ) pair も同時に定義されています。上で ⟨f,g⟩ と書かれていた射は今回入力した直積の定義では pair(f,g) と表記されます。 ファクトライザ pair 自体は射ではないので show で表示することは出来ず、 show function を使うことで型を表示できます。

cpl> show function pair
f0: *a -> *b  f1: *a -> *c
------------------------------
pair(f0,f1): *a -> prod(*b,*c)

また、prod は対象 a, b を対象 prod(a,b) に写すだけでなく、射 f: a -> c, g: b -> d を prod(a,b) -> prod(b,d) へと写します。圏論における 関手 (functor) は対象を対象に、対象の間の射を写された対象の間の射へと写します。 show function prod とすることで、 prod の射に対する作用の型を確認することができます。

cpl> show function prod
f0: *a -> *c  f1: *b -> *d
---------------------------------------
prod(f0,f1): prod(*a,*b) -> prod(*c,*d)

また、 equations を見ると、以下の4つの等式が成り立つことが分かります。なお、ここで使われている . は射の合成 (composition) を表す記法で、g.f は「まず f を適用し、次に g を適用する」という意味です（数学の記法 g ∘ f に対応します）。

指数対象の定義

次に、関数を値として扱うための構造である 指数対象 (exponential object) を定義します。

指数対象 Bᴬ (CPLでは exp(a,b) と表記) は「A から B への射全体を表す対象」です。これは以下の性質を持ちます:

図式として描くと以下のようになります：

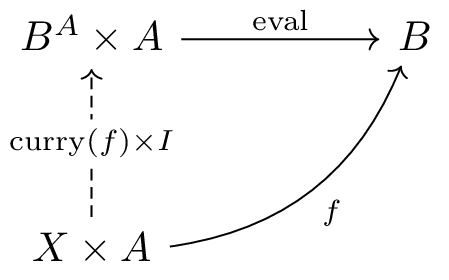
なぜ指数対象が「関数空間」なのか？ 集合の圏で具体的に考えてみましょう。

プログラミングとの対応:

終対象、直積、指数対象を備えた圏はカルテシアン閉圏 (Cartesian Closed Category) と呼ばれ、ラムダ計算や関数型プログラミングの理論的基礎となっています。

それでは、CPLで指数対象を定義します：

cpl> edit
| right object exp(a,b) with curry is
|   eval: prod(exp,a) -> b
| end object;
right object exp(-,+) defined

show object を使って詳細を表示してみます。

cpl> show object exp
right object exp(-,+)
- natural transformations:
    eval: prod(exp(*a,*b),*a) -> *b
- factorizer:
    f0: prod(*a,*b) -> *c
    ---------------------------
    curry(f0): *a -> exp(*b,*c)
- equations:
    (REQ1): eval.prod(curry(f0),I)=f0
    (RFEQ): exp(f0,f1)=curry(f1.eval.prod(I,f0))
    (RCEQ): eval.prod(g,I)=f0 => g=curry(f0)
- unconditioned: yes
- productive: (no,no)

関数適用を行う eval 、カリー化を行う curry 、圏論での指数対象の条件などが定義されていることが分かります。

show function を使って関手 exp の射に対する作用を確認してみましょう。

cpl> show function exp
f0: *c -> *a  f1: *b -> *d
------------------------------------
exp(f0,f1): exp(*a,*b) -> exp(*c,*d)

exp の引数となる射の向きと、exp のパラメータが始域から余域に変化する方向に注目してください。

しています。これは exp が第一引数について反変(contravariant)、第二引数について共変(covariant)な関手であることを意味しています。exp の定義時や show object exp で表示されていた exp(-,+) はこのことをコンパクトに表現した記法です。

自然数対象の定義

自然数対象 (natural numbers object) は、0と後続関数によって定義される帰納的な構造です。

自然数対象 ℕ は以下の要素によって特徴付けられます:

この pr (primitive recursion、原始再帰) は数学的帰納法に対応し、自然数上の関数を定義する基本的な方法です。

これを図式として描くと以下のようになります。

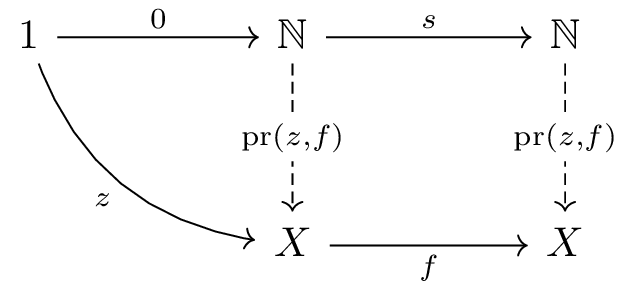
矢印の向きに注意してください。これまで取り扱ってきた終対象・直積・指数対象では、その対象を余域とする一意な射が存在したのに対して、自然数対象の場合には、逆にその対象を始域とする一意な射が存在します。

プログラミングとの対応:

それではCPLで自然数対象を定義しましょう。これまで扱ってきた、その対象を余域とする一意な射が存在する場合には right object として対象を定義していましたが、その対象を始域とする一意な射が存在する場合には left object として対象を定義します:

cpl> edit
| left object nat with pr is
|   0: 1 -> nat
|   s: nat -> nat
| end object;
left object nat defined

show object nat とすることで、情報を表示してみましょう。

cpl> show object nat
left object nat
- natural transformations:
    0: 1 -> nat
    s: nat -> nat
- factorizer:
    f0: 1 -> *a  f1: *a -> *a
    -------------------------
    pr(f0,f1): nat -> *a
- equations:
    (LEQ1): pr(f0,f1).0=f0
    (LEQ2): pr(f0,f1).s=f1.pr(f0,f1)
    (LFEQ): nat=pr(0,s)
    (LCEQ): g.0=f0 & g.s=f1.g => g=pr(f0,f1)
- unconditioned: no
- productive: ()

ゼロと後者関数を表す 0 と s 、また数学的帰納法に対応する pr およびそれらが満たすべき条件が定義されています。

直和の定義

直和 (coproduct) は、「どちらか一方」を表す構造で、直積の双対概念です。

直和 A + B (CPLでは coprod(a,b)) は、二つの対象 A と B のどちらか一方の値を持つ対象です:

これは直積の「矢印を逆にした」双対概念であり、圏論における対称性の良い例です。

図式で描くと以下のようになります（直積の図式と比較して、矢印が逆になっていることを確認してください）：

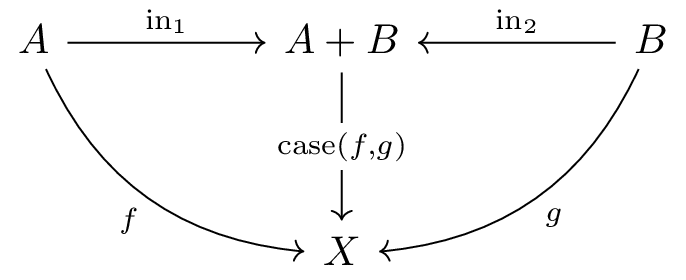
プログラミングとの対応:

それではCPLで直和を定義しましょう。

cpl> edit
| left object coprod(a,b) with case is
|   in1: a -> coprod
|   in2: b -> coprod
| end object;
left object coprod(+,+) defined
cpl> show object coprod
left object coprod(+,+)
- natural transformations:
    in1: *a -> coprod(*a,*b)
    in2: *b -> coprod(*a,*b)
- factorizer:
    f0: *b -> *a  f1: *c -> *a
    --------------------------------
    case(f0,f1): coprod(*b,*c) -> *a
- equations:
    (LEQ1): case(f0,f1).in1=f0
    (LEQ2): case(f0,f1).in2=f1
    (LFEQ): coprod(f0,f1)=case(in1.f0,in2.f1)
    (LCEQ): g.in1=f0 & g.in2=f1 => g=case(f0,f1)
- unconditioned: yes
- productive: (no,no)

型の表示

show コマンドを使って射の型(定義域と余域)を表示することができます。

cpl> show pair(pi2,eval)
pair(pi2,eval)
    : prod(exp(*a,*b),*a) -> prod(*a,*b)

*a や *b は対象を表す変数であり、このような射は実際には様々な型(定義域と余域)の射の族を表しています。この族がある条件を満たすときに 自然変換 (natural transformation) と呼ばれ、これは一般的な関数型言語における 多相関数 (polymorphic function) に対応する概念です。

上の例では、pair(pi2,eval) は任意の対象 *a と *b に対して機能する射であり、F(*a,*b) = prod(exp(*a,*b),*a) という関手から G(*a,*b) = prod(*a,*b) という関手への自然変換と考えることができます。

射の合成と恒等射

ここまでの定義で . という記号が等式の中に登場していましたが、ここで改めて射の基本操作を確認しておきましょう。

射の合成

. は射の合成 (composition) を表します。射 f: A → B と g: B → C があるとき、合成射 g.f: A → C は「まず f を適用し、次に g を適用する」射です。数学の記法 g ∘ f に対応します（Unicode記号 ∘ もCPLでは使用可能です）。

例えば、後続関数 s: nat → nat とゼロ 0: 1 → nat を合成することで、自然数を表現できます:

cpl> show s.0
s.0
    : 1 -> nat
cpl> show s.s.s.0
s.s.s.0
    : 1 -> nat

s.s.s.0 は「0 (ゼロ) に s (後続関数) を3回合成した射」で、自然数の 3 を表します。同様に s.s.0 は 2、s.0 は 1 です。

恒等射

恒等射 (identity morphism) I は「何もしない射」で、任意の対象 A に対して I: A → A が存在します:

cpl> show I
I
    : *a -> *a

恒等射は f.I = f かつ I.f = f を満たします。一見役に立たないようですが、関手と組み合わせて「一方の成分だけを変換し、他方はそのまま残す」際に頻繁に使います:

cpl> show prod(s, I)
prod(s,I)
    : prod(nat,*a) -> prod(nat,*a)

ここで prod(s, I) は「直積の第一成分に s を適用し、第二成分はそのまま」という射です。

式に名前を付ける

let コマンドを使うことで射に名前を付け、後から名前で参照することができます。これにより、複雑な射を段階的に構築できます。

最初の例として、自然数の加算 add: prod(nat, nat) → nat を定義しましょう。通常の関数型言語では以下のように書ける関数です:

add 0 y = y
add (x + 1) y = add x y + 1

CPLでは、これを原始再帰 pr とカリー化 curry を組み合わせて表現します。順を追って考えてみましょう。

  1. 方針: 第一引数について原始再帰 pr を使いたいが、pr(f0, f1): nat → X は一引数の射しか定義できません。そこでカリー化を使い、第二引数を指数対象の中に閉じ込めます

  2. カリー化された加算 add' を考える:

  3. f0 = curry(pi2) (ゼロの場合):

  4. f1 = curry(s.eval) (後続の場合):

  5. アンカリー化: add' = pr(curry(pi2), curry(s.eval)) を eval と prod で元に戻す

以上をまとめると:

cpl> let add=eval.prod(pr(curry(pi2), curry(s.eval)), I)
add : prod(nat,nat) -> nat  defined

let では、パラメータを持つ射の定義も行うことができます。

cpl> let uncurry(f) = eval . prod(f, I)
f: *a -> exp(*b,*c)
-----------------------------
uncurry(f): prod(*a,*b) -> *c

計算

CPLでは simp コマンドによって、射の式を簡約することで計算を行います。先ほど定義した加算の関数 add を使った射を簡約してみましょう。

cpl> simp add.pair(s.s.0, s.0)
s.s.s.0
    : 1 -> nat

この結果 s.s.s.0 は、後続関数 s を3回適用したもので、自然数の3を表しています。つまり、2 + 1 = 3 という計算が行われました。

加算と同様に、乗算と階乗も定義して計算してみましょう。

乗算 mult: prod(nat, nat) → nat は加算と同じパターン（カリー化 + 原始再帰 + アンカリー化）で定義できます:

cpl> let mult=eval.prod(pr(curry(0.!), curry(add.pair(eval, pi2))), I)
mult : prod(nat,nat) -> nat

add との違いはゼロの場合と再帰ステップだけです:

階乗 fact: nat → nat は少し異なる方法を使います。pr で prod(nat, nat) の状態（累積値とカウンタのペア）を持ち運びます:

cpl> let fact=pi1.pr(pair(s.0,0), pair(mult.pair(s.pi2,pi1), s.pi2))
fact : nat -> nat  defined

計算してみましょう:

cpl> simp fact.s.s.s.s.0
s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.0
    : 1 -> nat

s が24回適用されているので、4! = 24 という正しい結果が得られています。

リスト型

次は自然数とほぼ同じですが、少しだけ複雑なデータ型であるリスト型を定義してみます。

リストは自然数と同様に帰納的な構造を持ちますが、要素の型をパラメータとして持つ点が異なります:

図式を描くと以下のようになります。

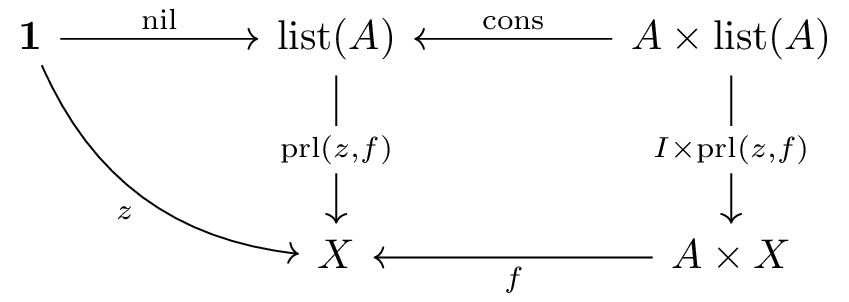
これは帰納的データ型の典型例で、有限の構造を表現します。

プログラミングとの対応:

それではCPLでリストを定義してみましょう。

cpl> edit
| left object list(p) with prl is
|   nil: 1 -> list
|   cons: prod(p,list) -> list
| end object;
left object list(+) defined
cpl> show function list
f0: *a -> *b
------------------------------
list(f0): list(*a) -> list(*b)
cpl> show object list
left object list(+)
- natural transformations:
    nil: 1 -> list(*a)
    cons: prod(*a,list(*a)) -> list(*a)
- factorizer:
    f0: 1 -> *a  f1: prod(*b,*a) -> *a
    ----------------------------------
    prl(f0,f1): list(*b) -> *a
- equations:
    (LEQ1): prl(f0,f1).nil=f0
    (LEQ2): prl(f0,f1).cons=f1.prod(I,prl(f0,f1))
    (LFEQ): list(f0)=prl(nil,cons.prod(f0,I))
    (LCEQ): g.nil=f0 & g.cons=f1.prod(I,g) => g=prl(f0,f1)
- unconditioned: no
- productive: (no)

リストも対象によってパラメータ化された対象、関手となっています。リストの射に対する作用について確認してみましょう。リスト関手の射に対する作用は関数型プログラミングではしばしば map と呼ばれています。

cpl> show function list
f0: *a -> *b
------------------------------
list(f0): list(*a) -> list(*b)

次にリスト型を用いたお馴染みの関数達を表現してみましょう。

連結（append）:

cpl> let append = eval.prod(prl(curry(pi2), curry(cons.pair(pi1.pi1, eval.pair(pi2.pi1, pi2)))), I)
append : prod(list(*a),list(*a)) -> list(*a)  defined

逆転（reverse）:

cpl> let reverse=prl(nil, append.pair(pi2, cons.pair(pi1, nil.!)))
reverse : list(*a) -> list(*a)  defined

head / tail:

cpl> let hd = prl(in2, in1.pi1)
hd : list(*a) -> coprod(*a,1)  defined
cpl> let tl = coprod(pi2,I).prl(in2, in1.prod(I, case(cons,nil)))
tl : list(*a) -> coprod(list(*a),1)  defined

後で無限リストを使う際に head / tail という名前を使いたいので、ここでは hd / tl という名前を使っています。また、CPLでは全域関数しか存在せず部分関数は存在しないため、余域は1との直和（他の言語における Maybe 型や Option 型）になっています。

さらに、 head / tail の結果に再度 head / tail を適用するのに便利なように、定義域を 1 との直和に持ち上げたバージョンも定義しておきましょう。

cpl> let hdp=case(hd,in2)
hdp : coprod(list(*a),1) -> coprod(*a,1)  defined
cpl> let tlp = case(tl, in2)
tlp : coprod(list(*a),1) -> coprod(list(*a),1)  defined

連番 [n-1, n-2, ..., 1, 0]:

cpl> let seq = pi2.pr(pair(0,nil), pair(s.pi1, cons))
seq : nat -> list(nat)  defined

これらを利用して計算を行ってみます。

一部の計算では simp だけでは簡約が進まないため、 simp full を使う必要があります。

cpl> simp seq.s.s.s.0
cons.pair(s.pi1,cons).pair(s.pi1,cons).pair(0,nil)
    : 1 -> list(nat)
cpl> simp full seq.s.s.s.0
cons.pair(s.s.0,cons.pair(s.0,cons.pair(0,nil)))
    : 1 -> list(nat)

simp だけでは中間的な形で止まりますが、simp full で完全に簡約されます。結果の cons.pair(s.s.0,cons.pair(s.0,cons.pair(0,nil))) は、CPLにおけるリストの表現です。これは他の言語で書けば [2, 1, 0] に対応します:

CPLの表現 意味
nil [] (空リスト)
cons.pair(x, xs) x : xs (x を xs の先頭に追加)
cons.pair(s.s.0, cons.pair(s.0, cons.pair(0, nil))) [2, 1, 0]

他の関数の計算結果も見てみましょう:

cpl> simp hdp.tl.seq.s.s.s.0
in1.s.0
    : 1 -> coprod(nat,*a)

seq.s.s.s.0 は [2, 1, 0] なので、tl で先頭を除いた [1, 0] に対し hdp で先頭を取ると in1.s.0 (= Just 1) になります。

cpl> simp full append.pair(seq.s.s.0, seq.s.s.s.0)
cons.pair(s.0,cons.pair(0,cons.pair(s.s.0,cons.pair(s.0,cons.pair(0,nil)))))
    : 1 -> list(nat)
cpl> simp full reverse.it
cons.pair(0,cons.pair(s.0,cons.pair(s.s.0,cons.pair(0,cons.pair(s.0,nil.!)))))
    : 1 -> list(nat)

append.pair(seq.s.s.0, seq.s.s.s.0) は [1, 0] と [2, 1, 0] の連結で [1, 0, 2, 1, 0] に、reverse.it はその逆転で [0, 1, 2, 0, 1] になります。

最後の例 simp full reverse.it では、it を使って直前の計算結果（append.pair(seq.s.s.0, seq.s.s.s.0) の結果）を参照しています。it は直前の simp コマンドの結果を自動的に保存する便利な機能です。

simp と simp full の違い

CPLには二つの簡約コマンドがあります:

無限リスト

自然数やリストのような有限のデータ型だけでなく、無限リストのデータ型を定義することもできます。

無限リストは、有限リストとは異なり right object として定義されます。これは余帰納的データ型 (coinductive type) の例です:

有限リストが「構築して消費する」のに対し、無限リストは「状態から展開していく」という対照的な構造を持ちます。

図式を描くと以下のようになります。

プログラミングとの対応:

それではCPLで無限リストを定義しましょう。

cpl> edit
| right object inflist(a) with fold is
|   head: inflist -> a
|   tail: inflist -> inflist
| end object;
right object inflist(+) defined
cpl> show object inflist
right object inflist(+)
- natural transformations:
    head: inflist(*a) -> *a
    tail: inflist(*a) -> inflist(*a)
- factorizer:
    f0: *a -> *b  f1: *a -> *a
    ------------------------------
    fold(f0,f1): *a -> inflist(*b)
- equations:
    (REQ1): head.fold(f0,f1)=f0
    (REQ2): tail.fold(f0,f1)=fold(f0,f1).f1
    (RFEQ): inflist(f0)=fold(f0.head,tail)
    (RCEQ): head.g=f0 & tail.g=g.f1 => g=fold(f0,f1)
- unconditioned: no
- productive: (no)

それでは、無限リストを用いた射の定義と計算をしてみましょう。

まず、0, 1, 2, 3, … という増加列を作ります:

cpl> let incseq=fold(I,s).0
incseq : 1 -> inflist(nat)  defined

fold(I,s) は「現在の状態をそのまま head として出力し (I)、状態に s を適用して次へ進む」という展開規則です。初期状態 0 から始めると、0, 1, 2, 3, … という無限列になります。

cpl> simp head.incseq
0
    : 1 -> nat
cpl> simp head.tail.tail.tail.incseq
s.s.s.0
    : 1 -> nat

head で先頭要素 0 を、head.tail.tail.tail で4番目の要素 3 を取り出せます。

次に、二つの無限リストを交互に組み合わせる alt を定義します:

cpl> let alt=fold(head.pi1, pair(pi2, tail.pi1))
alt : prod(inflist(*a),inflist(*a)) -> inflist(*a)  defined

alt は直積 prod(inflist, inflist) を状態として、head.pi1 で第一リストの先頭を出力し、pair(pi2, tail.pi1) で二つのリストの役割を入れ替えます（第二を先に、第一のtailを後に）。

cpl> let infseq=fold(I,I).0
infseq : 1 -> inflist(nat)  defined
cpl> simp head.tail.tail.alt.pair(incseq, infseq)
s.0
    : 1 -> nat

infseq は 0, 0, 0, … という定数列です。alt.pair(incseq, infseq) は 0, 0, 1, 0, 2, 0, 3, … と交互に並べた列になるため、3番目の要素（0始まりで index 2）は s.0 (= 1) です。

圏論的背景: left と right

CPLでデータ型を定義する際、left object と right object という二種類の宣言方法があります。これは圏論における重要な概念である双対性 (duality) を反映しています。

right object（終対象的構造）

right object は圏論における極限 (limit) に基づいた構造です。極限は「他の対象から入ってくる射によって特徴付けられる」という性質を持ちます。

left object（始対象的構造）

left object は圏論における余極限 (colimit) に基づいた構造です。余極限は「この対象から他の対象へ出ていく射によって特徴付けられる」という性質を持ちます。

どちらを使うべきか

一般的な指針:

しかし、圏論における left と right の対称性は深遠で、CPLを使いながらこの双対性を体感できることがCPLの大きな特徴の一つです。

圏論との対応

この left/right の区別は、圏論における以下の概念と対応しています:

CPL 圏論 性質
right object 極限 (limit)、右随伴 (right adjoint)、F-余代数 (F-coalgebra) 普遍射により「入射」を統一
left object 余極限 (colimit)、左随伴 (left adjoint)、F-代数 (F-algebra) 余普遍射により「出射」を統一

CPLでは、これらの概念が対称的に扱われ、圏論の理論が実際のプログラミングにどのように活用されるかを学ぶことができます。

まとめ

このチュートリアルを通じて、CPLの基本的な使い方と、圏論の基本概念を学びました。

学んだこと

CPLの使い方:

圏論の概念:

CPLのユニークな特徴

CPLでは、他のプログラミング言語では「組み込み」として提供される構造（数値、リスト、関数など）を、すべて圏論の概念を用いて明示的に定義します。これにより:

次のステップ

CPLをさらに深く学ぶために、以下を試してみてください:

  1. サンプルファイルの探索
  2. より複雑なプログラムを書く
  3. 圏論を学ぶ
  4. 他の圏論的プログラミング

参考文献

CPLの理論的基礎

圏論の入門書

オンラインリソース

関連する概念

このチュートリアルが、CPLと圏論の世界への第一歩となれば幸いです。楽しいプログラミングを!