CPL Tutorial

Introduction

CPL (Categorical Programming Language) is a programming language designed based on concepts from category theory. In CPL, what are typically referred to as “data types” and “functions” in conventional programming languages are instead treated as “objects” and “morphisms” (or “arrows”) in category theory.

Key Features of CPL

• Category-theoretic data type definition: All data types are defined using category theory concepts, specifically F,G-dialgebras—a generalization of adjunctions and F-(co)algebras
• Type safety: A robust type system grounded in category theory principles
• Functional programming: Only total functions are supported, ensuring pure computation without side effects
• Duality: Symmetric design using both left object (initial structure) and right object (terminal structure)

Prerequisite Knowledge

For optimal understanding, familiarity with the following:

• Basic programming concepts
• Experience with functional programming languages like Haskell (though not mandatory)

No prior knowledge of category theory is required. Through this tutorial, you’ll learn both CPL usage and fundamental category theory concepts.

What You’ll Learn from This Tutorial

• Basic CPL operations: REPL usage, data type definition, and function definition
• Fundamental category theory concepts: Terminal/initial objects, products/coproducts, exponential objects, etc.
• The distinction between left objects and right objects, and the concept of duality in category theory
• Practical programming examples: Natural numbers, lists, infinite lists, etc.

Table of Contents

• Introduction
• Basic Commands
• Initial Screen Display
• Defining Terminal Objects
• Defining Cartesian Products
• Defining Exponential Objects
• Defining the Natural Numbers Object
• Defining Coproducts
• Displaying Types
• Composing Morphisms and Identity Morphisms
• Assigning Names to Expressions
• Computation
• List Types
• Infinite Lists
• Category Theory Background: Left vs. Right
• Summary
• References

Basic Commands

The CPL REPL (Read-Eval-Print Loop) supports the following commands. This section provides only an overview, with detailed usage examples to be learned through practical application.

• edit: Enters multi-line editing mode. Use this for defining data types. End editing mode by entering semicolon (;)
• show <expression>: Displays the type (domain and codomain) of an morphism (function)
• show object <functor>: Displays detailed information about an object (data type)
• show function <function>: Displays the type of a factorizer (higher-order function) or user-defined function
• let <name> = <expression>: Defines an morphism by assigning it a name
• let <name>(<arguments>) = <expression>: Defines an morphism with parameters
• simp <expression>: Simplifies (computes) the given expression
• simp full <expression>: Fully simplifies the expression (use when simp alone cannot complete simplification)
• it: Refers to the result from the previous computation
• load <filename>: Loads definitions from a file
• help: Displays help information
• exit: Exits the CPL environment

Initial Screen

Upon startup, the interface appears as follows:

Categorical Programming Language (Haskell version)
version 0.1.0

Type help for help

cpl>

Defining the Terminal Object

CPL has no built-in data types, and all data types must be explicitly defined.

Since every operation requires the terminal object—corresponding to the unit type in other functional programming languages—we begin by defining this fundamental concept.

In category theory, a terminal object 1 is defined as “an object such that for every object X, there is exactly one morphism from X to 1.” It serves as an “endpoint” representing an object with no information (or containing only one value). The unique morphism is written as !.

Visually, this corresponds to the following situation:

Correspondences to programming concepts:

• Haskell’s () type (unit type)
• void or unit types in other languages
• The concept of “a type containing exactly one value”

Now, let’s define the terminal object in CPL. Using the edit command, enter multi-line editing mode, input your data type definition, and exit multi-line editing mode by entering semicolon ;.

cpl> edit
| right object 1 with !
| end object;
right object 1 defined

The output “right object 1 defined” confirms that the terminal object 1 has been successfully defined.

Detailed information about a defined object can be viewed using show object.

cpl> show object 1
right object 1
- natural transformations:
- factorizer:

    ----------
    !: *a -> 1
- equations:
    (RFEQ): 1=!
    (RCEQ): g=!
- unconditioned: yes
- productive: ()

When object 1 is defined, a special morphism ! is also defined from any object to the terminal object.

The show command can also be used to display the morphism’s type (domain and codomain). Here, *a is a variable representing an object, so this represents an morphism from any object to the terminal object 1.

cpl> show !
!
    : *a -> 1

Defining the Product

Next, we’ll define the product. The product combines two objects into a single object.

In category theory, the product A × B (prod(a,b) in CPL) is defined as “an object that preserves the information of both objects A and B.” It satisfies the following properties:

• Existence of projection morphisms π₁: A × B → A and π₂: A × B → B
• For any object X with morphisms f: X → A and g: X → B to A and B respectively, there exists a unique morphism ⟨f,g⟩: X → A × B such that π₁ ∘ ⟨f,g⟩ = f and π₂ ∘ ⟨f,g⟩ = g (this kind of property is referred to as the universal property).

Visually represented as a diagram:

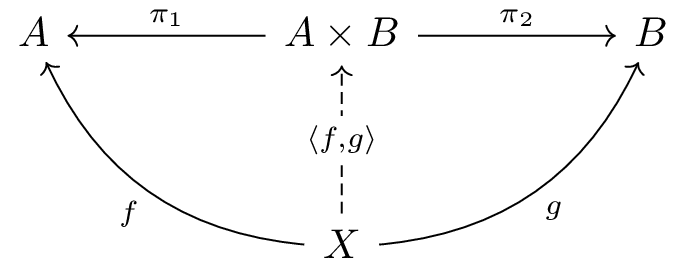
Correspondences with programming concepts:

• Haskell’s (a, b) type (tuple)
• Pairs or structures in other languages
• The concept of “a type that combines two values”

Now, let’s define the product in CPL:

cpl> edit
| right object prod(a,b) with pair is
|   pi1: prod -> a
|   pi2: prod -> b
| end object;
right object prod(+,+) defined

(Note in the definition of pi1 and pi2 that the object prod we’re defining now lacks arguments. The mearning is “Among all x equipped with x -> a and x -> b, we define the most general x as prod(a,b),” but reusing the name prod instead of introducing a new name x)

Unlike in the case of terminal objects, the product prod(a,b) is an object that takes parameters, and the resulting definition displays as prod(+,+). The + indicates covariance, and we can see that prod takes two arguments and is covariant with respect to both arguments. Use show object to display detailed information.

cpl> show object prod
right object prod(+,+)
- natural transformations:
    pi1: prod(*a,*b) -> *a
    pi2: prod(*a,*b) -> *b
- factorizer:
    f0: *a -> *b  f1: *a -> *c
    ------------------------------
    pair(f0,f1): *a -> prod(*b,*c)
- equations:
    (REQ1): pi1.pair(f0,f1)=f0
    (REQ2): pi2.pair(f0,f1)=f1
    (RFEQ): prod(f0,f1)=pair(f0.pi1,f1.pi2)
    (RCEQ): pi1.g=f0 & pi2.g=f1 => g=pair(f0,f1)
- unconditioned: yes
- productive: (yes,yes)

Unlike terminal objects, in the case of products, both projection morphisms pi1 and pi2 are defined simultaneously (you can also check their types using the show command).

Additionally, a function (factorizer) pair is also defined, which constructs pair(f,g): a -> prod(b,c) from f: a -> b and g: a -> c. The morphism previously written as ⟨f,g⟩ is now written as pair(f,g) in this definition of products in CPL. The factorizer pair itself is not an morphism and cannot be displayed using show; instead, use show function to display its type.

cpl> show function pair
f0: *a -> *b  f1: *a -> *c
------------------------------
pair(f0,f1): *a -> prod(*b,*c)

Furthermore, while prod maps objects a and b to the object prod(a,b), it also maps morphisms f: a -> c and g: b -> d to prod(a,b) -> prod(b,d). In category theory, a functor maps objects to objects and morphisms between objects to morphisms between mapped objects. Using show function prod, you can verify the type of prod’s action on morphisms.

cpl> show function prod
f0: *a -> *c  f1: *b -> *d
---------------------------------------
prod(f0,f1): prod(*a,*b) -> prod(*c,*d)

Furthermore, examining equations reveals that the following four equalities hold. Here, the . notation represents morphism composition, meaning g.f means “first apply f, then apply g” (corresponding to the mathematical notation g ∘ f).

• (REQ1): pi1.pair(f0,f1)=f0
  • (As stated earlier as a property of the product)
• (REQ2): pi2.pair(f0,f1)=f1
  • (Same as above)
• (RFEQ): prod(f0,f1)=pair(f0.pi1,f1.pi2)
  • (Definition of prod in terms of pair and pi1, pi2)
• (RCEQ): pi1.g=f0 & pi2.g=f1 => g=pair(f0,f1)
  • (If g satisfies the same conditions as pair(f0,f1), then g=pair(f0,f1), i.e., pair(f0,f1) is unique)

Definition of Exponential Object

Next, we define the exponential object, which is a structure for treating functions as values.

The exponential object Bᴬ (denoted as exp(a,b) in CPL) represents “the object that encodes all morphisms from A to B.” It possesses the following properties:

• An evaluation morphism eval: Bᴬ × A → B exists, allowing functions to be applied to values
  • (While we call it eval here, in functional programming contexts, apply would be a more natural name)
• For any morphism f: X × A → B, there exists a unique curried morphism curry(f): X → Bᴬ satisfying eval ∘ (curry(f) × I) = f
  • (Here, I: A → A represents the identity morphism, and × denotes the product morphism operation)

Visualized as a diagram, it appears as follows:

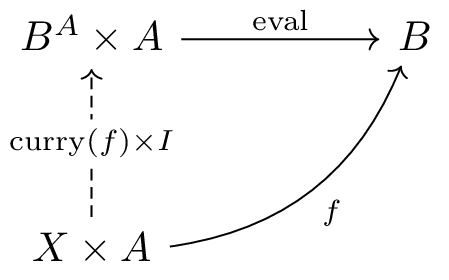
Why Is the Exponential Object Called a “Function Space”? Let’s consider this concretely in the context of the category of sets.

• Bᴬ is the set of all functions from A to B — In the category of sets, the exponential object Bᴬ is the set {f | f: A → B} of functions itself.
• eval represents function application — eval(f, a) = f(a). In other words, it performs the operation of “taking a pair of a function f and its argument a, and returning the result of applying f to a.”
• curry represents argument separation — For f: X × A → B, curry(f)(x) returns the function a ↦ f(x, a). In other words, currying transforms a two-argument function into a one-argument function that returns another function — this is precisely the operation of converting a function into a function that returns functions.
• Universality characterizes the function space — The commutativity of the diagram above — the property that “functions from X × A → B are in one-to-one correspondence with functions from X → Bᴬ” — is what uniquely characterizes Bᴬ as a function space. This correspondence is exactly the relationship between currying and function application in programming.

Correspondences with programming concepts:

• Haskell’s a -> b type (function type)
• Currying and function application
• The concept of “treating functions as first-class values”

A category equipped with the terminal object, product objects, and exponential objects is called a Cartesian Closed Category, which forms the theoretical foundation for lambda calculus and functional programming.

Now, let’s define the exponential object in CPL:

cpl> edit
| right object exp(a,b) with curry is
|   eval: prod(exp,a) -> b
| end object;
right object exp(-,+) defined

We can display detailed information using show object:

cpl> show object exp
right object exp(-,+)
- natural transformations:
    eval: prod(exp(*a,*b),*a) -> *b
- factorizer:
    f0: prod(*a,*b) -> *c
    ---------------------------
    curry(f0): *a -> exp(*b,*c)
- equations:
    (REQ1): eval.prod(curry(f0),I)=f0
    (RFEQ): exp(f0,f1)=curry(f1.eval.prod(I,f0))
    (RCEQ): eval.prod(g,I)=f0 => g=curry(f0)
- unconditioned: yes
- productive: (no,no)

We can see that eval for function application, curry for currying, and the conditions for an exponential object in category theory are all defined.

Let’s examine how the functor exp operates on morphisms using show function:

cpl> show function exp
f0: *c -> *a  f1: *b -> *d
------------------------------------
exp(f0,f1): exp(*a,*b) -> exp(*c,*d)

Note the directionality of the argument morphisms, and how the parameters of exp change from domain to codomain in the result:

• f0 is a morphism from *c to *a, but the parameter changes direction from *a to *c in the result
• f1 is a morphism from *b to *d, and the direction of the parameter is the same, from *b to *d

This indicates that exp is a contravariant functor with respect to the first argument and a covariant functor with respect to the second argument. The notation exp(-,+) used during definition and in show object exp is a concise representation of this property.

Definition of the Natural Numbers Object

A natural numbers object is an inductively defined structure characterized by the number 0 and the successor function.

The natural numbers object ℕ is uniquely characterized by the following elements:

• Zero 0: 1 → ℕ (the initial value)
• Successor function s: ℕ → ℕ (also denoted as succ, the function that increments by 1)
• For any object X and morphisms z: 1 → X and f: X → X, there exists a unique morphism pr(z,f): ℕ → X defined recursively such that pr(z,f) ∘ 0 = z and pr(z,f) ∘ s = f ∘ pr(z,f)

This pr operation corresponds to mathematical induction and serves as the fundamental method for defining functions over the natural numbers.

Visualized graphically, this structure appears as follows:

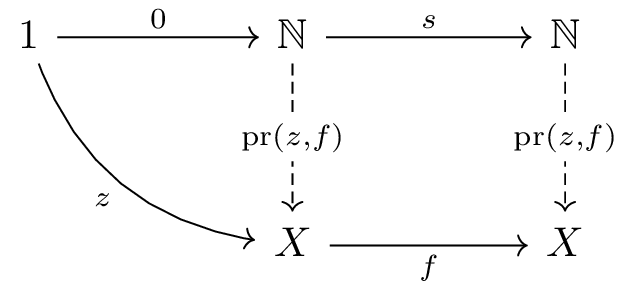
Please note the direction of the arrows. Whereas in the terminal objects, products, and exponential objects we have handled so far, there existed a unique morphism with that object as its codomain, in the case of the natural numbers object, conversely, there exists a unique morphism with that object as its domain.

Correspondences to programming concepts:

• The definition of natural numbers according to Peano’s axioms

• Equivalent to Haskell data types such as:

  data Nat = Zero | Succ Nat

• Recursive computations (folding)

Now, let’s define the natural numbers object in CPL. While we have previously defined objects as right objects when there exists a unique morphism with that object as their codomain, we now define the natural numbers object as left object as there exists a unique morphism with that object as their domain:

cpl> edit
| left object nat with pr is
|   0: 1 -> nat
|   s: nat -> nat
| end object;
left object nat defined

To display the defined information, use show object nat:

cpl> show object nat
left object nat
- natural transformations:
    0: 1 -> nat
    s: nat -> nat
- factorizer:
    f0: 1 -> *a  f1: *a -> *a
    -------------------------
    pr(f0,f1): nat -> *a
- equations:
    (LEQ1): pr(f0,f1).0=f0
    (LEQ2): pr(f0,f1).s=f1.pr(f0,f1)
    (LFEQ): nat=pr(0,s)
    (LCEQ): g.0=f0 & g.s=f1.g => g=pr(f0,f1)
- unconditioned: no
- productive: ()

Here, 0 and s represent the zero and successor functions respectively, while pr corresponds to mathematical induction, along with the conditions they must satisfy.

Defining the Coproduct

The coproduct is a structure representing “either-or,” serving as the dual concept to the direct product.

The coproduct A + B (denoted as coprod(a,b) in CPL) is an object that can hold one of two values, either from object A or B:

• It has two injection morphisms in₁: A → A + B and in₂: B → A + B (which “inject” values into the coproduct)
• For any objects X and morphisms f: A → X and g: B → X, there exists a unique morphism case(f,g): A + B → X that combines them case-by-case, satisfying case(f,g) ∘ in₁ = f and case(f,g) ∘ in₂ = g

This is the dual concept of the product, obtained by “reversing the arrow,” and serves as a good example of symmetry in category theory.

Visualized graphically, it appears as follows: (Compare with the product diagram to verify that morphisms are reversed):

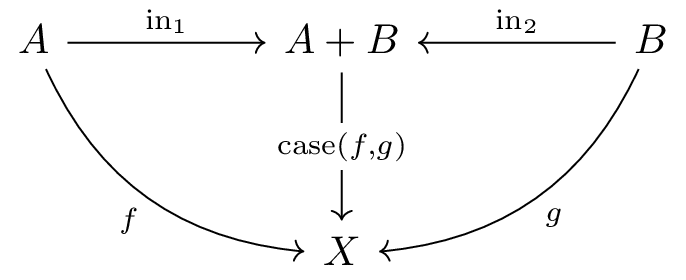
Correspondences to programming concepts:

• Haskell’s Either a b type
• variant types or other languages’ union types with tags
• Branching logic using pattern matching

Now let’s define the coproduct in CPL:

cpl> edit
| left object coprod(a,b) with case is
|   in1: a -> coprod
|   in2: b -> coprod
| end object;
left object coprod(+,+) defined

cpl> show object coprod
left object coprod(+,+)
- natural transformations:
    in1: *a -> coprod(*a,*b)
    in2: *b -> coprod(*a,*b)
- factorizer:
    f0: *b -> *a  f1: *c -> *a
    --------------------------------
    case(f0,f1): coprod(*b,*c) -> *a
- equations:
    (LEQ1): case(f0,f1).in1=f0
    (LEQ2): case(f0,f1).in2=f1
    (LFEQ): coprod(f0,f1)=case(in1.f0,in2.f1)
    (LCEQ): g.in1=f0 & g.in2=f1 => g=case(f0,f1)
- unconditioned: yes
- productive: (no,no)

Displaying Type Information

The show command can be used to display the types of morphisms (their domains and codomains).

cpl> show pair(pi2,eval)
pair(pi2,eval)
    : prod(exp(*a,*b),*a) -> prod(*a,*b)

Here, *a and *b are variable ranging over objects, and the morphism actually denotes families of morphisms with varying types (domains and codomains). When these families satisfy certain conditions, they are called natural transformations, which correspond to polymorphic functions in typical functional programming languages.

In the above example, pair(pi2,eval) is an morphism that works for any objects *a and *b, and can be viewed as a natural transformation from the functor F(*a,*b) = prod(exp(*a,*b),*a) to the functor G(*a,*b) = prod(*a,*b).

Morphism Composition and Identity Morphisms

The . symbol appearing in the equations above refers to fundamental operations on morphisms, which we will now review.

Morphism Composition

. represents morphism composition. Given morphisms f: A → B and g: B → C, the composed morphism g.f: A → C is the morphism that “first applies f, then applies g”. This corresponds to the mathematical notation g ∘ f (the Unicode symbol ∘ is also usable in CPL).

For example, we can represent natural numbers by composing the successor function s: nat → nat with the zero 0: 1 → nat:

cpl> show s.0
s.0
    : 1 -> nat
cpl> show s.s.s.0
s.s.s.0
    : 1 -> nat

s.s.s.0 represents the “morphism obtained by composing s (successor function) three times with 0”, which corresponds to the natural number 3. Similarly, s.s.0 represents 2, and s.0 represents 1.

Identity Morphisms

The identity morphism I is the “do-nothing” morphism, with I: A → A existing for any object A:

cpl> show I
I
    : *a -> *a

An identity morphism satisfies f.I = f and I.f = f. While it may seem trivial at first glance, we frequently use it in conjunction with functors to “transform only one of the components while leaving the other unchanged”:

cpl> show prod(s, I)
prod(s,I)
    : prod(nat,*a) -> prod(nat,*a)

Here, prod(s, I) represents the morphism that “applies s to the first component of the product while leaving the second component unchanged.”

Naming Expressions

The let command allows us to assign names to morphisms, enabling subsequent reference by name. This enables us to construct complex morphisms step by step.

As our first example, let’s define the natural number addition add: prod(nat, nat) → nat. This would be a function typically written as follows:

add 0 y = y
add (x + 1) y = add x y + 1

In CPL, we express this using primitive recursion pr combined with currying curry. Let’s break it down step by step.

1. Strategy: We want to use primitive recursion pr on the first argument, but pr(f0, f1): nat → X can only define unary morphisms. Therefore, we curry the second argument by encapsulating it within the exponential object.

2. Curried addition add':

   • add': nat → exp(nat, nat) — An morphism that takes a natural number n and returns a “function that adds n”
   • This can be defined in the form of pr(f0, f1)

3. f0 = curry(pi2) (zero case):

   • add'(0) returns “the function that adds 0” = the identity function
   • pi2: prod(1, nat) → nat is an morphism that extracts the second component of a product, which here functions as “discarding the first component (the unique value of the terminal object) while returning the second argument unchanged”
   • curry(pi2): 1 → exp(nat, nat) serves as the base case for the zero case

4. f1 = curry(s.eval) (successor case):

   • add'(n+1) returns “a function that applies s to the result of add'(n)”
   • eval: prod(exp(nat,nat), nat) → nat represents function application
   • s.eval: prod(exp(nat,nat), nat) → nat performs “function application followed by taking the successor”
   • curry(s.eval): exp(nat,nat) → exp(nat,nat) represents the recursive step

5. Uncurrying: Revert add' = pr(curry(pi2), curry(s.eval)) back to eval and prod:

   • prod(add', I): prod(nat, nat) → prod(exp(nat,nat), nat) — Applies add' to the first argument
   • eval.prod(add', I): prod(nat, nat) → nat — Applies the resulting function to the second argument

Putting it all together:

cpl> let add=eval.prod(pr(curry(pi2), curry(s.eval)), I)
add : prod(nat,nat) -> nat  defined

In the let construct, we can also define morphisms with parameters.

cpl> let uncurry(f) = eval . prod(f, I)
f: *a -> exp(*b,*c)
-----------------------------
uncurry(f): prod(*a,*b) -> *c

Computation

In CPL, computation is performed through simplification of morphism expressions using the simp command. Let’s simplify an morphism using our previously defined addition function add.

cpl> simp add.pair(s.s.0, s.0)
s.s.s.0
    : 1 -> nat

The result s.s.s.0 represents applying the successor function s three times, corresponding to the natural number 3. This demonstrates the calculation 2 + 1 = 3.

Similar to addition, let’s define and compute multiplication and factorial.

Multiplication mult: prod(nat, nat) → nat can be defined using the same pattern as addition (currying + primitive recursion + uncurrying):

cpl> let mult=eval.prod(pr(curry(0.!), curry(add.pair(eval, pi2))), I)
mult : prod(nat,nat) -> nat

The differences from add lie only in the zero case and the recursive step:

• Zero case curry(0.!) — 0 × y = 0 (0.! is an morphism that returns zero regardless of input)
• Successor case curry(add.pair(eval, pi2)) — (n+1) × y = n × y + y (adds the recursive result eval to y itself pi2)

Factorial fact: nat → nat uses a slightly different approach. It carries the state of prod(nat, nat) (a pair of accumulator and counter) using pr:

cpl> let fact=pi1.pr(pair(s.0,0), pair(mult.pair(s.pi2,pi1), s.pi2))
fact : nat -> nat  defined

• Initial value pair(s.0, 0) — (1, 0), i.e. “0! = 1, counter = 0”
• Recursive step pair(mult.pair(s.pi2, pi1), s.pi2) — computes (acc, k) to ((k+1) × acc, k+1)
• Final result pi1 extracts the accumulator value (the factorial result)

Let’s compute it:

cpl> simp fact.s.s.s.s.0
s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.s.0
    : 1 -> nat

Since s has been applied 24 times, we obtain the correct result 4! = 24.

List Type

Next, we’ll define a list type—a data structure that’s very similar to natural numbers but slightly more complex.

Lists, like natural numbers, have an inductive structure, but they differ in that lists are parameterized by their element type:

• Empty list nil: 1 → list(a)
• Element prepend cons: a × list(a) → list(a) (adds an element to the front)
• Fold prl(z,f): list(a) → b for recursively processing lists

Visualized graphically:

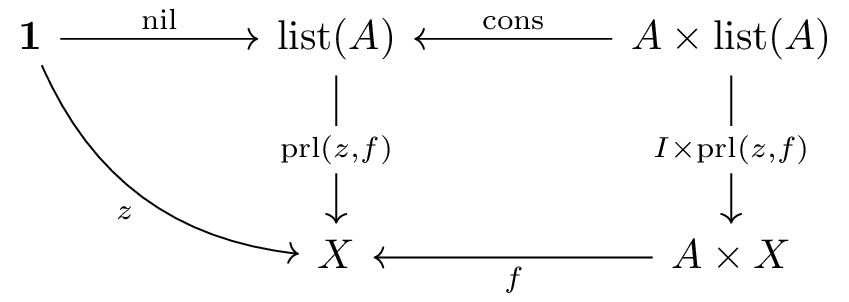
This represents a classic example of an inductive data type that describes finite structures.

Correspondence with programming:

• Haskell’s [a] type (lists)
• Folding using foldr

Now let’s define lists in CPL:

cpl> edit
| left object list(p) with prl is
|   nil: 1 -> list
|   cons: prod(p,list) -> list
| end object;
left object list(+) defined

cpl> show function list
f0: *a -> *b
------------------------------
list(f0): list(*a) -> list(*b)
cpl> show object list
left object list(+)
- natural transformations:
    nil: 1 -> list(*a)
    cons: prod(*a,list(*a)) -> list(*a)
- factorizer:
    f0: 1 -> *a  f1: prod(*b,*a) -> *a
    ----------------------------------
    prl(f0,f1): list(*b) -> *a
- equations:
    (LEQ1): prl(f0,f1).nil=f0
    (LEQ2): prl(f0,f1).cons=f1.prod(I,prl(f0,f1))
    (LFEQ): list(f0)=prl(nil,cons.prod(f0,I))
    (LCEQ): g.nil=f0 & g.cons=f1.prod(I,g) => g=prl(f0,f1)
- unconditioned: no
- productive: (no)

The list is also a parameterized object, that is, a functor. Let’s examine its action on morphisms. In functional programming, this action of the list functor on morphisms is often referred to as map.

cpl> show function list
f0: *a -> *b
------------------------------
list(f0): list(*a) -> list(*b)

Next, let’s express some familiar functions using the list type.

Concatenation (append):

cpl> let append = eval.prod(prl(curry(pi2), curry(cons.pair(pi1.pi1, eval.pair(pi2.pi1, pi2)))), I)
append : prod(list(*a),list(*a)) -> list(*a)  defined

Reversal (reverse):

cpl> let reverse=prl(nil, append.pair(pi2, cons.pair(pi1, nil.!)))
reverse : list(*a) -> list(*a)  defined

head / tail:

cpl> let hd = prl(in2, in1.pi1)
hd : list(*a) -> coprod(*a,1)  defined
cpl> let tl = coprod(pi2,I).prl(in2, in1.prod(I, case(cons,nil)))
tl : list(*a) -> coprod(list(*a),1)  defined

We’ve chosen hd / tl here because we want to use these names when working with infinite lists later. In CPL, since only total functions exist and no partial functions are allowed, the codomain is a coproduct with 1 (equivalent to the Maybe or Option types in other languages).

For convenience, we’ve also defined versions that lift the domain to the coproduct with 1, allowing us to apply head / tail to the results of these operations again.

cpl> let hdp=case(hd,in2)
hdp : coprod(list(*a),1) -> coprod(*a,1)  defined
cpl> let tlp = case(tl, in2)
tlp : coprod(list(*a),1) -> coprod(list(*a),1)  defined

Sequential numbers [n-1, n-2, ..., 1, 0]:

cpl> let seq = pi2.pr(pair(0,nil), pair(s.pi1, cons))
seq : nat -> list(nat)  defined

Now, let’s perform some computations.

Some calculations require simp full instead of just simp to proceed with reduction.

cpl> simp seq.s.s.s.0
cons.pair(s.pi1,cons).pair(s.pi1,cons).pair(0,nil)
    : 1 -> list(nat)
cpl> simp full seq.s.s.s.0
cons.pair(s.s.0,cons.pair(s.0,cons.pair(0,nil)))
    : 1 -> list(nat)

While simp alone stops at an intermediate form, simp full completes the full reduction. The result cons.pair(s.s.0,cons.pair(s.0,cons.pair(0,nil))) represents list notation in CPL. In other languages, this corresponds to the list [2, 1, 0]:

Let’s examine the results of computing with other functions as well:

cpl> simp hdp.tl.seq.s.s.s.0
in1.s.0
    : 1 -> coprod(nat,*a)

Since seq.s.s.s.0 equals [2, 1, 0], applying tl to remove the head yields [1, 0], and then applying hdp to get the head results in in1.s.0 (which equals Just 1).

cpl> simp full append.pair(seq.s.s.0, seq.s.s.s.0)
cons.pair(s.0,cons.pair(0,cons.pair(s.s.0,cons.pair(s.0,cons.pair(0,nil)))))
    : 1 -> list(nat)
cpl> simp full reverse.it
cons.pair(0,cons.pair(s.0,cons.pair(s.s.0,cons.pair(0,cons.pair(s.0,nil.!)))))
    : 1 -> list(nat)

append.pair(seq.s.s.0, seq.s.s.s.0) concatenates [1, 0] and [2, 1, 0] to form [1, 0, 2, 1, 0], while reverse.it reverses this to produce [0, 1, 2, 0, 1].

In the final example simp full reverse.it, we use it to reference the result of the previous computation (append.pair(seq.s.s.0, seq.s.s.s.0)). it is a useful feature that automatically stores the result of the immediately preceding simp command.

Differences Between simp and simp full

CPL provides two reduction commands:

• simp: Performs basic reduction. Fast but may stop prematurely
• simp full: Performs more thorough reduction. Use when a completely reduced form is required

Infinite Lists

In addition to finite data types like natural numbers and lists, we can also define data types for infinite lists.

Unlike finite lists, infinite lists are defined as a right object. This is an example of a coinductive data type:

• head: inflist(a) → a (extracts the head element)
• tail: inflist(a) → inflist(a) (obtains the remaining infinite list)
• fold(h,t): x → inflist(a) allows unfolding the infinite list (note that while named fold, in modern functional programming conventions this would more appropriately be called unfold)

While finite lists operate by “building up and then consuming,” infinite lists have the contrasting structure of “unfolding from state.”

Visualized graphically:

Corresponding to programming concepts:

• Haskell’s lazy evaluation-based infinite lists
• Streams and iterators
• Generation via unfold

Now let’s define an infinite list in CPL.

cpl> edit
| right object inflist(a) with fold is
|   head: inflist -> a
|   tail: inflist -> inflist
| end object;
right object inflist(+) defined

cpl> show object inflist
right object inflist(+)
- natural transformations:
    head: inflist(*a) -> *a
    tail: inflist(*a) -> inflist(*a)
- factorizer:
    f0: *a -> *b  f1: *a -> *a
    ------------------------------
    fold(f0,f1): *a -> inflist(*b)
- equations:
    (REQ1): head.fold(f0,f1)=f0
    (REQ2): tail.fold(f0,f1)=fold(f0,f1).f1
    (RFEQ): inflist(f0)=fold(f0.head,tail)
    (RCEQ): head.g=f0 & tail.g=g.f1 => g=fold(f0,f1)
- unconditioned: no
- productive: (no)

Now, let’s define and compute with morphisms using infinite lists.

First, we create an ascending sequence 0, 1, 2, 3, …:

cpl> let incseq=fold(I,s).0
incseq : 1 -> inflist(nat)  defined

fold(I,s) represents the unfolding rule that “outputs the current state as the head (I), then applies s to the state to proceed.” Starting from the initial state 0, this produces the infinite sequence 0, 1, 2, 3, …

cpl> simp head.incseq
0
    : 1 -> nat
cpl> simp head.tail.tail.tail.incseq
s.s.s.0
    : 1 -> nat

We can extract the first element 0 using head, and the fourth element 3 using head.tail.tail.tail.

Next, we define the alt function that alternates between two infinite lists:

cpl> let alt=fold(head.pi1, pair(pi2, tail.pi1))
alt : prod(inflist(*a),inflist(*a)) -> inflist(*a)  defined

alt uses the product prod(inflist, inflist) as its state, with head.pi1 outputting the head of the first list, and pair(pi2, tail.pi1) swapping the roles of the two lists (outputting the second list first, followed by the first list’s tail).

cpl> let infseq=fold(I,I).0
infseq : 1 -> inflist(nat)  defined
cpl> simp head.tail.tail.alt.pair(incseq, infseq)
s.0
    : 1 -> nat

infseq is a constant sequence 0, 0, 0, … The expression alt.pair(incseq, infseq) produces an alternating sequence 0, 0, 1, 0, 2, 0, 3, … Therefore, the third element (index 2 starting from 0) is s.0 (= 1).

Category-Theoretic Background: left and right

When defining data types in CPL, there are two types of declarations: left object and right object. This reflects the important concept of duality in category theory.

right object (terminal structure)

A right object is a structure based on limits in category theory. Limits are characterized by their property of being “defined by incoming morphisms from other objects.”

• Key characteristic: Morphisms from other objects to this one (incoming morphisms) are crucial
• Role of factorizer: Creates new morphisms by combining multiple morphisms
• Examples in CPL:
  • Terminal object 1: The unique morphism ! from any object to 1
  • Product prod(a,b): Creates morphism pair(f,g): x -> prod(a,b) from two morphisms f: x -> a and g: x -> b
  • Exponent object exp(a,b): Creates morphisms through currying
  • Infinite list inflist: Expands infinite structures using fold
• Correspondence to programming: Coinductive types, types whose values are determined by behavior, lazy evaluation

left object (initial structure)

A left object is a structure based on colimits in category theory. Colimits are characterized by their property of being “defined by outgoing morphisms from this object to others.”

• Key characteristic: Morphisms from this object to other objects (outgoing morphisms) are crucial
• Role of factorizer: Breaks down and consumes multiple cases
• Examples in CPL:
  • Natural numbers nat: Consumes (folds) natural numbers defined recursively by pr
  • Coproduct coprod(a,b): Branches into two cases using case
  • List list: Folds recursive list structures using prl
• Correspondence to programming: Inductive types, types whose values are determined by structure, pattern matching

Which one should be used?

General guidelines:

• Finite data structures: Use left object (constructed recursively)
• Infinite data structures: Use right object (expanded corecursively)

However, the symmetry between left and right in category theory is profound, and being able to experience this duality while using CPL is one of the language’s key features.

Correspondence to category theory

This left/right distinction corresponds to the following:

In CPL, these concepts are treated symmetrically, allowing you to learn how category theory concepts are applied in practical programming.

Summary

Through this tutorial, you’ve learned both the basic usage of CPL and fundamental category theory concepts.

What you’ve learned

CPL usage:

• Command operations in the REPL (edit, show, let, simp, etc.)
• Defining data types (objects and functors) using left object and right object
• Defining and combining morphisms
• Performing computation through expression simplification

Category theory concepts:

• Terminal/initial objects: The concept of “a point where all paths converge”
• Products/coproducts: The dual operations of “combining/selecting multiple pieces of information”
• Exponential objects: Structures that treat functions as values (Cartesian closed categories)
• Limits/colimits: Foundational concepts behind right object and left object
• Inductive/coinductive data types: The contrast between finite and infinite structures
• Duality: The symmetrical relationship between left and right in category theory

Unique features of CPL

In CPL, structures that would typically be “built-in” in other programming languages (such as numbers, lists, and functions) are all explicitly defined using category theory concepts. This results in:

• Direct connections between fundamental programming concepts and category theory
• Hands-on experience with left/right duality through actual code
• Understanding the mathematical structure underlying the type system

Next steps

To deepen your understanding of CPL, we recommend trying the following:

1. Exploring sample files
   • The samples/ directory contains various program examples
   • Try loading and executing samples using load “samples/examples.cpl”
2. Writing more complex programs
   • The Ackermann function (see samples/ack.cpl)
   • Other recursive functions and data structures
3. Studying category theory
   • Use the concepts learned in CPL as a starting point to read category theory textbooks
   • You’ll gain deeper understanding of concepts like limits, colimits, and adjoints
4. Exploring other category-theoretic programming
   • Revisit the type systems of other functional languages like Haskell from a category theory perspective
   • Applications to dependent type theory and proof assistants (Coq, Agda, etc.)

References

Theoretical foundations of CPL

• Tatsuya Hagino, “A Categorical Programming Language”, PhD Thesis, University of Edinburgh, 1987
  • The doctoral thesis that established the theoretical foundations of CPL
• Tatsuya Hagino, “Categorical Functional Programming Language”, Computer Software Vol 7 No.1, 1992
  • A paper explaining CPL’s overview in Japanese

Introductions to category theory

• Bartosz Milewski, “Category Theory for Programmers”
  • An introductory category theory textbook for programmers. Available free online.
• Steve Awodey, “Category Theory” (Oxford Logic Guides)
  • A more mathematically rigorous textbook on category theory

Online resources

• CPL WebAssembly version: https://msakai.github.io/cpl/
  • Allows you to try CPL directly in your browser
• GitHub repository: https://github.com/msakai/cpl
  • Contains source code, samples, and documentation

Related concepts

• Cartesian closed category: A category with products and exponential objects. The categorical model of lambda calculus.
• Adjunction: The central concept underlying left and right objects.
• Universal property: A key characteristic property in category theory that defines objects and morphisms.

We hope this tutorial serves as your first introduction to the world of CPL and category theory. Happy programming!